Study design and data source

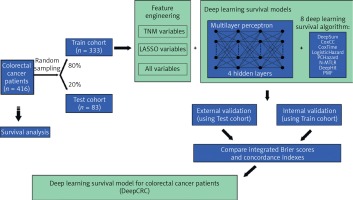
This study was designed as a retrospective cohort study. Patients diagnosed with colorectal cancer in 2006–2014 were included and the last follow-up time was 2018. Raw clinical information was obtained from the biobank of Shanghai Outdo Biotech Company. Multivariate Imputation by Chained Equations was employed to fill in missing values (Supplementary Figure S1). All data were then divided into two cohorts randomly (Figure 1): the training cohort (80% of all) and the test cohort (20% of all). Survival models were trained using the training cohort, with validation by itself and the test cohort.

Figure 1

Schematic diagram of this study

LASSO – Least Absolute Shrinkage and Selection Operator.

This study has been approved by the Ethics Committee (No. LW-2022-007) and individual consent for this retrospective analysis was waived.

Model training

Sex, age, size, site, grade, numbers of lymph nodes examined, numbers of positive lymph nodes, T, N, M and stage were all the clinical features included by the authors (abbreviated as ALL variables). Classical TNM variables (T, N, M and stage) were included as input features too, called TNM variables by us. Least Absolute Shrinkage and Selection Operator (LASSO) was adopted to refine variables, filtering non-zero coefficient features as LASSO variables (Age, Size, Site, Grade, Lymph nodes examined, Lymph nodes positive, T, N, M and Stage) (Supplementary Figure S2, Supplementary Table SI). Three group variables were then combined with 8 NN survival algorithms to identify the best one, with traditional Cox models conducted too as a comparison. Before building the models, categorical clinical features were recoded as dummy variables. The Adam algorithm was chosen to be an optimizer. Batch training and batch normalization were used to avoid underfitting, while dropout layers and the early stopping callback function were applied to avoid overfitting when necessary. Dropout layers could silence some neural nodes randomly and the early stopping callback function could end up training when performance did not improve during several epochs. Training curves are shown in Supplementary Figure S3.

Model evaluation

The concordance index (C-index), also known as area under the receiver operating curve (AUC), was the main criterion. The C-index close to 1.0 showed a perfect prediction, while a 0.5 or smaller one tended to randomly guess. Another indicator was the integrated Brier score, whose range was between 0 and 1, with a smaller one or near 0 representing a better performance. Each model was evaluated on the training cohort and test cohort. 1000 times bootstrap (resampling 1000 times from the training or test cohort) was taken to get precise 95% confidence intervals (CIs) of the C-index.

Data processing and statistical analysis

Missing values were visualized and imputation performed by R 4.1.2 with mice and VIM packages. LASSO regression was established with the R package glmnet. NN was constructed with python 3.9.7, pytorch and pycox. R packages (fmsb, RColorBrewer and ggplot2) were used for visualization. Two-sided p < 0.05 was considered statistically significant.

Patient characteristics

Patients diagnosed with CRC in 2006–2014 (n = 416) were stochastically split up into two groups, the training cohort (80% of all, n = 333) and test cohort (20% of all, n = 83) (Figure 1). Table I shows the clinical characteristics of the two cohorts. The median follow-up time of the training cohort was 62 months, with that of the test cohort being 65 months. There were 156 events observed in the training cohort and 30 in the test cohort.

Model performance

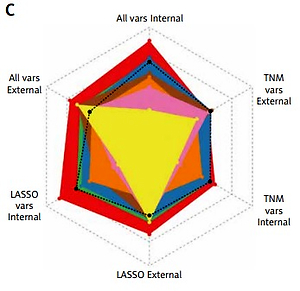
As illustrated in Figure 2 and Table II, TNM variables could not reflect a patient prognosis appropriately enough even using the NN algorithm, with a C-index between 0.4756–0.6957, of which DeepSurv behaved best. When LASSO variables were inputted, the performances were boosted markedly, with the top C-index up to 0.8224 in the training cohort and 0.7491 in the test cohort, from DeepSurv too. All variables were employed to conduct models finally, making some enhancement, for the C-index was determined as 0.8300 in the training cohort and 0.7681 in the test cohort by DeepSurv. Of 3 groups, ALL variables seemed to be the best indicator while DeepSurv showed the greatest potency in predicting patient OS.

Figure 2

Performance of 8 neural network algorithms combined with 3 group variables, both internal and external validations. A – The Brier score of them. B – The concordance index of them. C – The radar plot showing the comparison of concordance index among these combinations

C-index – concordance index. TNM vars – T + N + M + Stage. LASSO vars – Age + Size + Site + Grade + Lymph nodes examined + Lymph nodes positive + T + N + M + Stage. All vars – Sex + Age + Size + Site + Grade + Lymph nodes examined + Lymph nodes positive + T + N + M + Stage. CoxCC – Cox Case-control Corresponding methods. PCHazard – Piecewise Constant Hazard. N-MTLR – Neural Multi-Task Logistic Regression. PMF – Probability Mass Function. LASSO – Least Absolute Shrinkage and Selection Operator.

After 1000 times bootstrap, DeepSurv still exhibited the best performance, with the C-index 0.8315 (95% CIs: 0.8297–0.8332) in the training cohort and 0.7719 (95% CIs: 0.7693–0.7745) in the test cohort (Supplementary Table SII).